Tracer le cercle avec l'équerre
+5
Logos
VillaChicoubis
Charly Alverda
Laposse
Calcédoine
9 participants
A la croisée des chemins :: Les sujets du blogforum :: Sujets connexes :: Géométrie et mathématique sacrées
Page 1 sur 2
Page 1 sur 2 • 1, 2 
 Tracer le cercle avec l'équerre
Tracer le cercle avec l'équerre
Dans le fil où nous examinons la gravure  Melencolia I, réalisée par
Melencolia I, réalisée par  Albrecht Dürer (1471-1528), Charly Alverda propose cette possible énigme :
Albrecht Dürer (1471-1528), Charly Alverda propose cette possible énigme :
Si seulement une corde était aussi disponible…
D'abord tracer une droite et y placer un point (vers le milieu, par commodité). Une droite s'obtient par exemple au moyen d'un fil à plomb, ou en tendant une corde entre deux piquets fichés en terre.
Puis, grâce au compas planté dans le point choisi, on trace un cercle. Ce qui nous intéresse, ce sont les intersections de ce cercle avec notre droite d'origine. Ces intersections déterminent deux nouveaux points intéressants.

Donnons un bon écartement bien large à notre compas (par exemple le diamètre du cerle précédent, mais pas obligatoirement), et plantons-le successivement sur l'un puis l'autre des deux intersections déterminées précédemment. Traçons deux cercles identiques. Entre leurs deux intersections, en haut et en bas, tendons à nouveau une corde pour tirer une droite. Cette dernière est exactement perpendiculaire à la première. Deux planches de bois posées selon ces deux droites permettent aisément de construire une belle équerre, grâce uniquement à un compas et deux bouts de ficelle.
Maintenant, reste à décrire la démarche inverse : construire un cercle au départ d'une équerre... autrement qu'en plantant une extrémité de l'équerre pour s'en servir comme compas !
 Melencolia I, réalisée par
Melencolia I, réalisée par  Albrecht Dürer (1471-1528), Charly Alverda propose cette possible énigme :
Albrecht Dürer (1471-1528), Charly Alverda propose cette possible énigme :Hiram, artiste peintre de Tradition Optique et de formation Académique, mais aussi pour qui l'ésotérisme est un principe et une voie, propose de redécouvrir cette technique de tracé :Il me vient à l’idée que nous considérons normalement que la fonction du compas est de tracer des cercles, mais pour le Compagnonnage un compas ne sert qu’à mesurer et l’on trace un cercle avec l’équerre ! C’était du moins encore vrai au début du XVIIe siècle.
J'ignore si Charly a employé une métaphore, ou si les compagnons avaient réellement mis au point une technique concrète de tracé d'un cercle avec seulement une équerre…Hiram a écrit:J’ai une suggestion amicale pour vous, Charly, comme tous les Frères et les Sœurs réunis à ce carrefour qui n’ont pas les œuvres de Desargues. Je ne les ai pas non plus; peut-être pourriez-vous nous faire la démonstration de l’équerre construisant le cercle. Je propose que nous puissions être vos disciples pour cette manœuvre.
Si seulement une corde était aussi disponible…
| Intrigué, je viens de replonger dans le roman d'Henri Vincenot "Les Etoiles de Compostelle". L'histoire se passe au XIIIème siècle et raconte un voyage vers St-Jacques de Compostelle qui est prétexte à l'initiation de Jehan le Tonnerre aux mystères des Compagnons constructeurs. L'ouvrage contient de multiples schémas illustrant les techniques de tracé de différentes figures géométriques au moyen d'instruments simples (un compas et une corde). Mais je n'y ai pas trouvé la solution. Au contraire, j'ai trouvé la méthode de construction d'une équerre (donc, d'un angle droit entre deux droites) au moyen d'un compas. Mais là, nous sommes dans le dessin classique élémentaire, tel qu'on l'enseigne dans tous les collèges. |  |
D'abord tracer une droite et y placer un point (vers le milieu, par commodité). Une droite s'obtient par exemple au moyen d'un fil à plomb, ou en tendant une corde entre deux piquets fichés en terre.
Puis, grâce au compas planté dans le point choisi, on trace un cercle. Ce qui nous intéresse, ce sont les intersections de ce cercle avec notre droite d'origine. Ces intersections déterminent deux nouveaux points intéressants.

Donnons un bon écartement bien large à notre compas (par exemple le diamètre du cerle précédent, mais pas obligatoirement), et plantons-le successivement sur l'un puis l'autre des deux intersections déterminées précédemment. Traçons deux cercles identiques. Entre leurs deux intersections, en haut et en bas, tendons à nouveau une corde pour tirer une droite. Cette dernière est exactement perpendiculaire à la première. Deux planches de bois posées selon ces deux droites permettent aisément de construire une belle équerre, grâce uniquement à un compas et deux bouts de ficelle.
Maintenant, reste à décrire la démarche inverse : construire un cercle au départ d'une équerre... autrement qu'en plantant une extrémité de l'équerre pour s'en servir comme compas !

Calcédoine- Admin
- Nombre de messages : 325
Date d'inscription : 02/04/2008
 Re: Tracer le cercle avec l'équerre
Re: Tracer le cercle avec l'équerre
 Bonjour !
Bonjour !Je pense que planter l'équerre pour tracer un cercle afin d'éviter l'usage du compas relève de la
 logique shadok !
logique shadok !
Par contre, il doit bien exister une manière de résoudre cette quadrature du cercle, puisque le svastika, symbole connu depuis plusieurs millénaires, nous montre l'équerre en rotation :

Cherchons donc…

Laposse- Nombre de messages : 242
Age : 55
Date d'inscription : 05/04/2008
 Re: Tracer le cercle avec l'équerre
Re: Tracer le cercle avec l'équerre
Bonjour,
Avant de revenir à Désargues, voici un extrait d’essai que j’ai en chantier pour remettre les “pendules à Salomon”... à l’heure !
Compagnonnages
Ce sont les clercs du Moyen-Age qui ont rédigé les premiers règlements des bâtisseurs, établissant à dessein une tradition mythique où le merveilleux et les anachronismes s’entremêlent, dans le but de pacifier les “oeuvriers” en les rendant fiers de leur métier par le lien d’une tradition immémoriale. Les grandes figures de l’histoire sont bien présentes dans ces textes, la toute première en importance est bien sur Euclide le père de la géométrie puis le roi Salomon pour la construction, on évoque Nabuchodosor mais aussi Pythagore. Les clercs décident de tout, les maçons exécutent, puis viendra le temps où les religieux retourneront dans leurs monastères et où le Maître maçon aux gants blancs et à la Règle graduée apparaîtra.
Le mot français « compagnonnage » est inévitablement contemporain de celui de “franc-maçon” apparaissant dans le Discours de Ramsay, ces deux termes n'apparaissent qu’au début du XVIIIe siècle. Au XVIIe siècle, c’est celui de “devoirs” qui prévalait dans le langage des constructeurs, le mot compagnonnage impliquant seulement la durée du travail que le compagnon devait faire chez un maître avant de travailler pour son propre compte.
Les archives compagnonniques qui ne remontent guère avant le XVIIIe siècle, font référence à trois fondateurs légendaires : le Roi Salomon qui pour les récompenser de leurs travaux, leur donna un Devoir (une doctrine), puis Maître Jacques et le père Soubise. Les deux derniers auraient travaillé à la construction du Temple de Salomon, mais les textes bibliques qui la mentionnent sont muets à cet égard.
Au XVIIIe siècle, certains “Compagnons” ne savaient plus vraiment à quel Maître ils se référaient. Une légende, identifiait Maître Jacques au dernier grand-maître de l'Ordre du Temple : Jacques de Molay, une autre l'identifiait à Jacques Moler, qui aurait été maître d'œuvre de la cathédrale d'Orléans en 1401. Cette dernière date est significative, dans une autre légende compagnonnique elle est celle de la séparation des rites. Lors de la construction des tours de la Cathédrale Sainte-Croix d'Orléans, deux maîtres d'œuvre, Jacques Moler et Soubise de Nogent se seraient opposés lors d’une grève suivie d’une bataille amenant la scission. Il est vraisemblable qu’il y ait là confusion entre scission rituelle et scission confessionaliste, car c’est la destruction par les compagnons de la flèche de la cathédrale d'Orléans en 1568 qui entraîna la scission avec les compagnons catholiques. Encore selon les légendes, le père Soubise (qu’on représente toujours en robe de bure), Maître charpentier sur le chantier du Temple de Salomon, aurait été à l'origine de l'assassinat de Maître Jacques, bien que d'autres légendes l'en innocentent.
On comprend alors que beaucoup de Compagnons à la recherche de leurs origines se soient initiés très tôt à la Franc-maçonnerie d’obédience, et il y eut échange entre ces deux “sociétés”. Le mythe d’Hiram était apparu vers 1675 dans les textes maçonniques et il entre dans les “cayennes” vers la fin du XVIIIe siècle pour se répandre dans tous les compagnonnages au siècle suivant.
Revenons à Désargues. Il est aux premières “loges” pour parler des “devoirs”, je n’ai pas d’exemple plus ancien de cette connaissance ; il traduit les termes de métiers des “ouvriers” et leurs pratiques pour améliorer les rapports (forcément) houleux entre l’architecte qui symboliquement a tué leurs maîtres, bien qu’il donne le titre de “maître masson” aux “compagnons”.
pour parler des “devoirs”, je n’ai pas d’exemple plus ancien de cette connaissance ; il traduit les termes de métiers des “ouvriers” et leurs pratiques pour améliorer les rapports (forcément) houleux entre l’architecte qui symboliquement a tué leurs maîtres, bien qu’il donne le titre de “maître masson” aux “compagnons”.
C’est dans un de ses livres (consultables sur le Net) que j’ai lu que les “ouvriers de l’ancienne mode” traçaient des cercles avec l’équerre”, ce qui m’avait fort intrigué, mais ne donnant pas la pratique (sans doute parce qu’il la trouvait sans intérêt) j’en avais déduit que le compas était en ces temps avant tout un instrument de mesure. Mon hypothèse subsidiaire est que le compas d’appareillage était adapté aux mesures des pierres et sachant que l’équerre était le plus important outil des tailleurs, j’étais resté sur ma fin.
A l’attention du “petit Hiram (qui) arrive sur le forum Melencolia I” et à qui je répondrai bientôt sur l’autre fil, je n’ai jamais prétendu pouvoir faire la démonstration de l’équerre construisant le cercle, j’ai simplement cité un fait relaté par un témoin digne de crédit. N’ayant pas besoin de maître car je suis un homme libre, “franc”, je n’ai pas besoin de disciple(s)
J’ai recherché un peu, c’est laborieux ! dans “La pratique du trait à preuves” :
 http://architectura.cesr.univ-tours.fr/traite/Notice/MBAT1950-7-1.asp
http://architectura.cesr.univ-tours.fr/traite/Notice/MBAT1950-7-1.asp
Mais c’est peut-être dans :
 “Brouillon project d'une atteinte aux evenemens des rencontres du cône avec un plan"
“Brouillon project d'une atteinte aux evenemens des rencontres du cône avec un plan"
écrit dans un langage emprunté à la "langue de bois" des compagnons charpentiers, c’est-à-dire les signes de marquage des pièces de charpente, les orientant sur le chantier.
Ou pire dans sa correspondance, tout est sur le Net, faut chercher ! Et pis on n’est SURTOUT pas obligé de me croire, na !

Cordialement,
C...a
Non, je n’ai pas employé de métaphore, Hiram me paraissant très motivé dans l’étude des “devoirants” et citant Désargues, j’avais cru qu’il connaissait cette pratique, c’est pourquoi je la rappelais.Calcédoine a écrit:J'ignore si Charly a employé une métaphore, ou si les compagnons avaient réellement mis au point une technique concrète de tracé d'un cercle avec seulement une équerre…
Avant de revenir à Désargues, voici un extrait d’essai que j’ai en chantier pour remettre les “pendules à Salomon”... à l’heure !
Compagnonnages
Ce sont les clercs du Moyen-Age qui ont rédigé les premiers règlements des bâtisseurs, établissant à dessein une tradition mythique où le merveilleux et les anachronismes s’entremêlent, dans le but de pacifier les “oeuvriers” en les rendant fiers de leur métier par le lien d’une tradition immémoriale. Les grandes figures de l’histoire sont bien présentes dans ces textes, la toute première en importance est bien sur Euclide le père de la géométrie puis le roi Salomon pour la construction, on évoque Nabuchodosor mais aussi Pythagore. Les clercs décident de tout, les maçons exécutent, puis viendra le temps où les religieux retourneront dans leurs monastères et où le Maître maçon aux gants blancs et à la Règle graduée apparaîtra.
Le mot français « compagnonnage » est inévitablement contemporain de celui de “franc-maçon” apparaissant dans le Discours de Ramsay, ces deux termes n'apparaissent qu’au début du XVIIIe siècle. Au XVIIe siècle, c’est celui de “devoirs” qui prévalait dans le langage des constructeurs, le mot compagnonnage impliquant seulement la durée du travail que le compagnon devait faire chez un maître avant de travailler pour son propre compte.
Les archives compagnonniques qui ne remontent guère avant le XVIIIe siècle, font référence à trois fondateurs légendaires : le Roi Salomon qui pour les récompenser de leurs travaux, leur donna un Devoir (une doctrine), puis Maître Jacques et le père Soubise. Les deux derniers auraient travaillé à la construction du Temple de Salomon, mais les textes bibliques qui la mentionnent sont muets à cet égard.
Au XVIIIe siècle, certains “Compagnons” ne savaient plus vraiment à quel Maître ils se référaient. Une légende, identifiait Maître Jacques au dernier grand-maître de l'Ordre du Temple : Jacques de Molay, une autre l'identifiait à Jacques Moler, qui aurait été maître d'œuvre de la cathédrale d'Orléans en 1401. Cette dernière date est significative, dans une autre légende compagnonnique elle est celle de la séparation des rites. Lors de la construction des tours de la Cathédrale Sainte-Croix d'Orléans, deux maîtres d'œuvre, Jacques Moler et Soubise de Nogent se seraient opposés lors d’une grève suivie d’une bataille amenant la scission. Il est vraisemblable qu’il y ait là confusion entre scission rituelle et scission confessionaliste, car c’est la destruction par les compagnons de la flèche de la cathédrale d'Orléans en 1568 qui entraîna la scission avec les compagnons catholiques. Encore selon les légendes, le père Soubise (qu’on représente toujours en robe de bure), Maître charpentier sur le chantier du Temple de Salomon, aurait été à l'origine de l'assassinat de Maître Jacques, bien que d'autres légendes l'en innocentent.
On comprend alors que beaucoup de Compagnons à la recherche de leurs origines se soient initiés très tôt à la Franc-maçonnerie d’obédience, et il y eut échange entre ces deux “sociétés”. Le mythe d’Hiram était apparu vers 1675 dans les textes maçonniques et il entre dans les “cayennes” vers la fin du XVIIIe siècle pour se répandre dans tous les compagnonnages au siècle suivant.
Revenons à Désargues. Il est aux premières “loges”
C’est dans un de ses livres (consultables sur le Net) que j’ai lu que les “ouvriers de l’ancienne mode” traçaient des cercles avec l’équerre”, ce qui m’avait fort intrigué, mais ne donnant pas la pratique (sans doute parce qu’il la trouvait sans intérêt) j’en avais déduit que le compas était en ces temps avant tout un instrument de mesure. Mon hypothèse subsidiaire est que le compas d’appareillage était adapté aux mesures des pierres et sachant que l’équerre était le plus important outil des tailleurs, j’étais resté sur ma fin.
A l’attention du “petit Hiram (qui) arrive sur le forum Melencolia I” et à qui je répondrai bientôt sur l’autre fil, je n’ai jamais prétendu pouvoir faire la démonstration de l’équerre construisant le cercle, j’ai simplement cité un fait relaté par un témoin digne de crédit. N’ayant pas besoin de maître car je suis un homme libre, “franc”, je n’ai pas besoin de disciple(s)
J’ai recherché un peu, c’est laborieux ! dans “La pratique du trait à preuves” :
 http://architectura.cesr.univ-tours.fr/traite/Notice/MBAT1950-7-1.asp
http://architectura.cesr.univ-tours.fr/traite/Notice/MBAT1950-7-1.aspMais c’est peut-être dans :
 “Brouillon project d'une atteinte aux evenemens des rencontres du cône avec un plan"
“Brouillon project d'une atteinte aux evenemens des rencontres du cône avec un plan"écrit dans un langage emprunté à la "langue de bois" des compagnons charpentiers, c’est-à-dire les signes de marquage des pièces de charpente, les orientant sur le chantier.
Ou pire dans sa correspondance, tout est sur le Net, faut chercher ! Et pis on n’est SURTOUT pas obligé de me croire, na !
Cordialement,
C...a
Charly Alverda- Nombre de messages : 534
Date d'inscription : 02/10/2008
 Re: Tracer le cercle avec l'équerre
Re: Tracer le cercle avec l'équerre
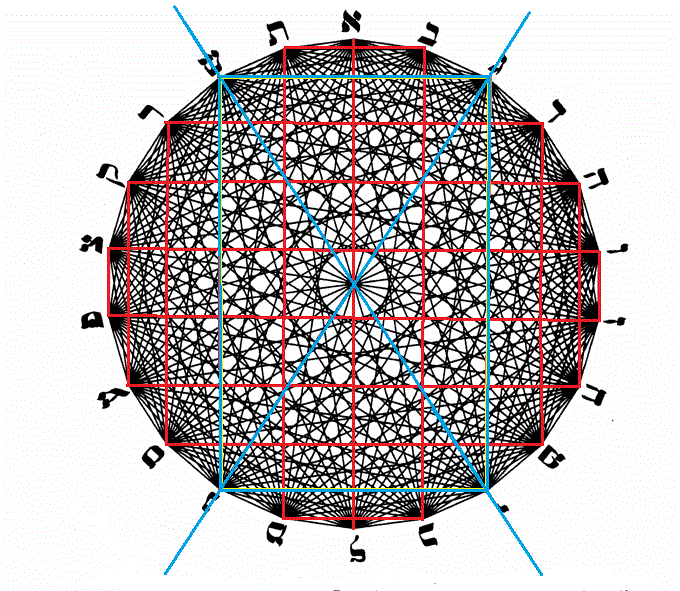
Voilà un cercle tracé à l'équerre sur la base de 22 lettres à l'intérieur duquel se forment 10 cercles (les 10 séphiroth) + L'invisible qu'on ne voit que par émanation : la 11éme séphirah = daath. C'est un cercle kabbaliste réalisé sans compas...



VillaChicoubis- Nombre de messages : 83
Date d'inscription : 21/02/2012
 Re: Tracer le cercle avec l'équerre
Re: Tracer le cercle avec l'équerre
Salut Villa-chic-à-chic
Juste pour vérifier : les cercles apparaissent-ils "naturellement" au cours du tracé, comme un ensemble de "noeuds" très denses ?
J'ai du mal à en distinguer 10 par contre, pourrais-tu par exemple marquer d'un repère coloré ?
En tout merci c'est intéressant
Juste pour vérifier : les cercles apparaissent-ils "naturellement" au cours du tracé, comme un ensemble de "noeuds" très denses ?
J'ai du mal à en distinguer 10 par contre, pourrais-tu par exemple marquer d'un repère coloré ?
En tout merci c'est intéressant

Logos- Nombre de messages : 551
Date d'inscription : 23/12/2009
 Re: Tracer le cercle avec l'équerre
Re: Tracer le cercle avec l'équerre
Bonjour.
Je les vois bien, ces cercles. J'en ai tracé un ici en rouge, les autres lui sont parallèles.
Ce ne sont pas tout à fait de "vrais" cercles, puisque ce sont des figures formées par des portions de traits droits (polygones à 20 côtés), mais visuellement, l'effet est similaire, surtout au plus près du centre.
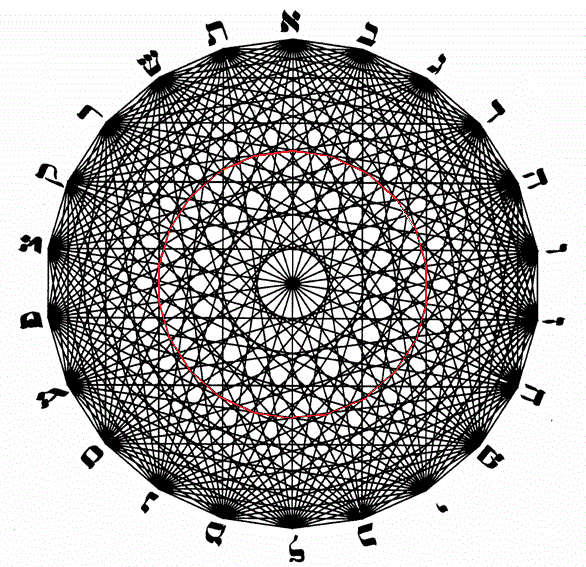
L'apparition des 10 cercles est une réalité mathématique facile à comprendre.
Il y a 22 lettres.
Au départ de chacune, vers chaque autre, on tire des droites, donc 21 traits droits par lettre.
Un de ces traits est destiné à la lettre située à l'opposé du cercle; il passe donc par le centre. Ces 22 diamètres forment les rayons de la roue.
Par lettre, il reste donc 20 autres traits à répartir de part et d'autre de ce diamètre : dix d'un côté, dix de l'autre.
Ce sont les portions de ces 10 traits qui se combinent pour former les 10 cercles concentriques.
En réduisant la taille de l'image ou en se reculant très loin de l'écran, on ne voit pratiquement plus qu'eux !
Un nombre de lettres différent aurait engendré un nombre différent de cercles concentriques.
VillaChicoubis nous apporte donc ici la preuve géométrique d'une relation mathématique entre les 22 lettres de l'alphabet hébreu et les 10 séphiroth.
Je les vois bien, ces cercles. J'en ai tracé un ici en rouge, les autres lui sont parallèles.
Ce ne sont pas tout à fait de "vrais" cercles, puisque ce sont des figures formées par des portions de traits droits (polygones à 20 côtés), mais visuellement, l'effet est similaire, surtout au plus près du centre.

L'apparition des 10 cercles est une réalité mathématique facile à comprendre.
Il y a 22 lettres.
Au départ de chacune, vers chaque autre, on tire des droites, donc 21 traits droits par lettre.
Un de ces traits est destiné à la lettre située à l'opposé du cercle; il passe donc par le centre. Ces 22 diamètres forment les rayons de la roue.
Par lettre, il reste donc 20 autres traits à répartir de part et d'autre de ce diamètre : dix d'un côté, dix de l'autre.
Ce sont les portions de ces 10 traits qui se combinent pour former les 10 cercles concentriques.
En réduisant la taille de l'image ou en se reculant très loin de l'écran, on ne voit pratiquement plus qu'eux !
Un nombre de lettres différent aurait engendré un nombre différent de cercles concentriques.
VillaChicoubis nous apporte donc ici la preuve géométrique d'une relation mathématique entre les 22 lettres de l'alphabet hébreu et les 10 séphiroth.

Montaléchel- Nombre de messages : 173
Date d'inscription : 25/07/2008
 Re: Tracer le cercle avec l'équerre
Re: Tracer le cercle avec l'équerre
Et il est aussi démontré qu'on peut faire des cercles avec juste : Une équerre.
Symbole de l'échelle de jacob = Ascension des 10 séphiroth puisque par 32 sont les chemins de la sagesse : 22 lettres et 10 chiffres (Voir sepher yetsirah - version gra - qui est le texte de kabbale hébraique qui pose les lois de l'arbre séphirothique)
Le tracé de base consiste, avec une équerre, à dessiner à la base une simple croix, et à rediviser par deux les quartiers, puis encore par deux les 08émes obtenus. Puis à relier les 22 points obtenus.
Les 10 cercles émergent tout seuls.
Et le 11ème est lumineux, il apparaît et se voit si on se concentre sur la figure qui nous entraîne dans un petit délire spirituel si on sait y faire.
Pour être fidèle et citer la source : Je tiens cette figure d'un ami juif (je suis moi même catholique mais par la voie du noachisme toutes les connexions et interconnexions se révèlent possibles). Cet ami juif est adepte de la haute magie kabbaliste. On le remercie donc pour cette publication qui, avec son accord, peut profiter à tous.
Symbole de l'échelle de jacob = Ascension des 10 séphiroth puisque par 32 sont les chemins de la sagesse : 22 lettres et 10 chiffres (Voir sepher yetsirah - version gra - qui est le texte de kabbale hébraique qui pose les lois de l'arbre séphirothique)
Le tracé de base consiste, avec une équerre, à dessiner à la base une simple croix, et à rediviser par deux les quartiers, puis encore par deux les 08émes obtenus. Puis à relier les 22 points obtenus.
Les 10 cercles émergent tout seuls.
Et le 11ème est lumineux, il apparaît et se voit si on se concentre sur la figure qui nous entraîne dans un petit délire spirituel si on sait y faire.
Pour être fidèle et citer la source : Je tiens cette figure d'un ami juif (je suis moi même catholique mais par la voie du noachisme toutes les connexions et interconnexions se révèlent possibles). Cet ami juif est adepte de la haute magie kabbaliste. On le remercie donc pour cette publication qui, avec son accord, peut profiter à tous.

VillaChicoubis- Nombre de messages : 83
Date d'inscription : 21/02/2012
 Re: Tracer le cercle avec l'équerre
Re: Tracer le cercle avec l'équerre
En fait en écrivant :
"Le tracé de base consiste, avec une équerre, à dessiner à la base une simple croix, et à rediviser par deux les quartiers, puis encore par deux les 08èmes obtenus. Puis à relier les 22 points obtenus."
Je pensais que quelques-uns parmi vous allaient se mettre à dessiner, pour venir ensuite me faire oberver que mon explication ne tient pas la route... Si on part d'une croix en effet on obtient des huitiémes, des seizièmes, des trente-deuxièmes mais pas de vingt-deuxièmes !!!...
Ce à quoi j'aurais répondu : En effet elle ne tient pas la route, c'était pour voir si vous alliez essayer...
Car ce n'est pas tout de regarder ce dessin en se disant simplement : Oui les cercles tracés à l'équerre existent.... Il faut s'y essayer pour comprendre que tirer les lignes, c'est simple.... Quand on a réussi au préalable à fixer dans le vide 22 points de repère en cercle, posés tous à la même distance.
Et ce juste avec une équerre.....
Alors je vous invite tous à vous confronter à l'expérience, une feuille blanche, 01 équerre, et juste avec cela, fixer dans le vide 22 points en cercle parfait...
Et pourquoi je vous invite à le faire ?... Tout simplement car si je raconte tout, vous ne connaîtrez pas cette grande émotion personnelle qui est celle du "eurêka bingo j'ai trouvé"... D'autant que cette émotion dans le contexte de l'émanation des 32 chemins de la sagesse, peut vous entraîner dans des expériences de pensée intéressantes...
Les mathématiques sacrées répondent à une norme qui est celle de la dialectique des âmes. Elles ne sont pas conçues pour faire décoller des fusées, mais pour faire décoller les âmes. Elles correspondent également à une certaine logique de construction du voyage initiatique... Cet instant précieux où l'élève qui a bien travaillé, voit enfin arriver le maître.
Bien à vous tous...
"Le tracé de base consiste, avec une équerre, à dessiner à la base une simple croix, et à rediviser par deux les quartiers, puis encore par deux les 08èmes obtenus. Puis à relier les 22 points obtenus."
Je pensais que quelques-uns parmi vous allaient se mettre à dessiner, pour venir ensuite me faire oberver que mon explication ne tient pas la route... Si on part d'une croix en effet on obtient des huitiémes, des seizièmes, des trente-deuxièmes mais pas de vingt-deuxièmes !!!...
Ce à quoi j'aurais répondu : En effet elle ne tient pas la route, c'était pour voir si vous alliez essayer...
Car ce n'est pas tout de regarder ce dessin en se disant simplement : Oui les cercles tracés à l'équerre existent.... Il faut s'y essayer pour comprendre que tirer les lignes, c'est simple.... Quand on a réussi au préalable à fixer dans le vide 22 points de repère en cercle, posés tous à la même distance.
Et ce juste avec une équerre.....
Alors je vous invite tous à vous confronter à l'expérience, une feuille blanche, 01 équerre, et juste avec cela, fixer dans le vide 22 points en cercle parfait...
Et pourquoi je vous invite à le faire ?... Tout simplement car si je raconte tout, vous ne connaîtrez pas cette grande émotion personnelle qui est celle du "eurêka bingo j'ai trouvé"... D'autant que cette émotion dans le contexte de l'émanation des 32 chemins de la sagesse, peut vous entraîner dans des expériences de pensée intéressantes...
Les mathématiques sacrées répondent à une norme qui est celle de la dialectique des âmes. Elles ne sont pas conçues pour faire décoller des fusées, mais pour faire décoller les âmes. Elles correspondent également à une certaine logique de construction du voyage initiatique... Cet instant précieux où l'élève qui a bien travaillé, voit enfin arriver le maître.
Bien à vous tous...

VillaChicoubis- Nombre de messages : 83
Date d'inscription : 21/02/2012
 Re: Tracer le cercle avec l'équerre
Re: Tracer le cercle avec l'équerre
Bonjour VillaChicoubis,
J'avoue avoir découvert ta proposition première avec un certain étonnement, car j'imaginais aisément tracer à l'équerre un polygone doté d'un nombre de faces égal à une puissance de 2, soit 4, 8, 16, 32 côtés...

Ça m'avait intrigué, puis, boulot et fatiguent obligent, j'avais laissé cette bizarrerie "de côté".

Tu reviens aujourd'hui à la charge, non sans bon sens, avec de la suite dans les idées.
Le théorème de Gauss-Wantzel nous dit :
Exemple A : 20 = 22 x 5
Un polygone à 20 côtés est possible
Exemple B : 24 = 23 x 3
Un polygone à 24 côtés est possible
Dans notre cas, 22 n'étant divisible ni par 3 ni par 5 (et encore moins par 17 ou 257), je ne vois pas comment on pourrait tracer ce polygone avec équerre et compas.
Si, en plus, le jeu exige qu'on se passe du compas, alors, on est mal barré !
Sauf...
Sauf si on peut aborder le problème sous l'angle du "changement de paradigme" : ne pas utiliser l'équerre et la feuille uniquement dans un seul plan, mais éventuellement plier la feuille de papier, sortir de la logique 2D et penser en 3D, comme dans le cas de L'occultisme des allumettes ?
L'occultisme des allumettes ?
J'avoue avoir découvert ta proposition première avec un certain étonnement, car j'imaginais aisément tracer à l'équerre un polygone doté d'un nombre de faces égal à une puissance de 2, soit 4, 8, 16, 32 côtés...
Ça m'avait intrigué, puis, boulot et fatiguent obligent, j'avais laissé cette bizarrerie "de côté".

Tu reviens aujourd'hui à la charge, non sans bon sens, avec de la suite dans les idées.
Le théorème de Gauss-Wantzel nous dit :
Un nombre de Fermat premier est, dans l'état actuel de nos connaissances mathématiques, un nombre de cette liste : 3, 5, 17, 257, 65537Un polygone à n côtés est constructible à la règle et au compas si et seulement si n est le produit d'une puissance de 2 et de k nombres de Fermat premiers tous différents.
Exemple A : 20 = 22 x 5
Un polygone à 20 côtés est possible
Exemple B : 24 = 23 x 3
Un polygone à 24 côtés est possible
Dans notre cas, 22 n'étant divisible ni par 3 ni par 5 (et encore moins par 17 ou 257), je ne vois pas comment on pourrait tracer ce polygone avec équerre et compas.
Si, en plus, le jeu exige qu'on se passe du compas, alors, on est mal barré !
Sauf...

Sauf si on peut aborder le problème sous l'angle du "changement de paradigme" : ne pas utiliser l'équerre et la feuille uniquement dans un seul plan, mais éventuellement plier la feuille de papier, sortir de la logique 2D et penser en 3D, comme dans le cas de
 L'occultisme des allumettes ?
L'occultisme des allumettes ?
Montaléchel- Nombre de messages : 173
Date d'inscription : 25/07/2008
 Re: Tracer le cercle avec l'équerre
Re: Tracer le cercle avec l'équerre
Bon là je suis larguée car moi les maths j'ai abandonné à l'age de l'équation à une inconnue....
Par contre je me souviens d'un ami kabbaliste, un juif qui pratiquait l'échelle de jacob et qui me disait en ce temps là : "le scientifique a du mal à monter la montagne, il souffre du froid, glisse sur la glace, se retrouve aux pieds de barres infranchissables, et quand enfin amaigri et enfièvré il parvient au sommet, il découvre une bande de théologiens occupés à boire le thé en l'attendant"...
En fait je crois que pour résoudre ce probléme mathématique, il faut renoncer à toute science, et être simplement un peu superstitieux...
Il y a dans les nombres, des nombres étranges qui ne répondent pas aux mêmes normes de logique que les autres ? Et si la solution était tout simplement dans ces nombres ?
N'oubliez pas que ceux qui ont inventé ces choses-là n'avaient pas d'ordinateur... Juste une feuille et une équerre. On ne peut pas faire grand chose de la feuille surtout au temps des parchemins... Par contre l'équerre, elle, peut être étudiée...
Bien à vous tous.... Je laisse la pression monter un peu dans les cocottes avant d'en dire plus...
Par contre je me souviens d'un ami kabbaliste, un juif qui pratiquait l'échelle de jacob et qui me disait en ce temps là : "le scientifique a du mal à monter la montagne, il souffre du froid, glisse sur la glace, se retrouve aux pieds de barres infranchissables, et quand enfin amaigri et enfièvré il parvient au sommet, il découvre une bande de théologiens occupés à boire le thé en l'attendant"...
En fait je crois que pour résoudre ce probléme mathématique, il faut renoncer à toute science, et être simplement un peu superstitieux...
Il y a dans les nombres, des nombres étranges qui ne répondent pas aux mêmes normes de logique que les autres ? Et si la solution était tout simplement dans ces nombres ?
N'oubliez pas que ceux qui ont inventé ces choses-là n'avaient pas d'ordinateur... Juste une feuille et une équerre. On ne peut pas faire grand chose de la feuille surtout au temps des parchemins... Par contre l'équerre, elle, peut être étudiée...
Bien à vous tous.... Je laisse la pression monter un peu dans les cocottes avant d'en dire plus...

VillaChicoubis- Nombre de messages : 83
Date d'inscription : 21/02/2012
 Re: Tracer le cercle avec l'équerre
Re: Tracer le cercle avec l'équerre
Juste pour faire avancer le schmilblick...
L'équerre, tu la vois comment ?
Je suppose qu'il s'agit d'un simple croisement de deux planches droites avec un angle droit (90°), et qu'il ne s'agit pas d'un instrument sophistiqué pourvu d'angles supplémentaires (30° et 60°) ou de graduations.
Et pas avec une pointe, pour s'en servir comme compas, comme proposé (absurdement, bien sûr, par votre serviteur) :
 J'demande ça, juste pour être sûr...
J'demande ça, juste pour être sûr...
Et, pour la culture générale, découvrons qu'un polygone à 22 côtés a un nom : Doicosagone.
Doicosagone.
 Pas sûr que ce soit vraiment utile...
Pas sûr que ce soit vraiment utile...
L'équerre, tu la vois comment ?
Je suppose qu'il s'agit d'un simple croisement de deux planches droites avec un angle droit (90°), et qu'il ne s'agit pas d'un instrument sophistiqué pourvu d'angles supplémentaires (30° et 60°) ou de graduations.
Et pas avec une pointe, pour s'en servir comme compas, comme proposé (absurdement, bien sûr, par votre serviteur) :

Et, pour la culture générale, découvrons qu'un polygone à 22 côtés a un nom :
 Doicosagone.
Doicosagone. Pas sûr que ce soit vraiment utile...
Pas sûr que ce soit vraiment utile...
Laposse- Nombre de messages : 242
Age : 55
Date d'inscription : 05/04/2008
 Re: Tracer le cercle avec l'équerre
Re: Tracer le cercle avec l'équerre
Pourtant, on observe dans cette figure tout un réseau de parallèles et de perpendiculaires 
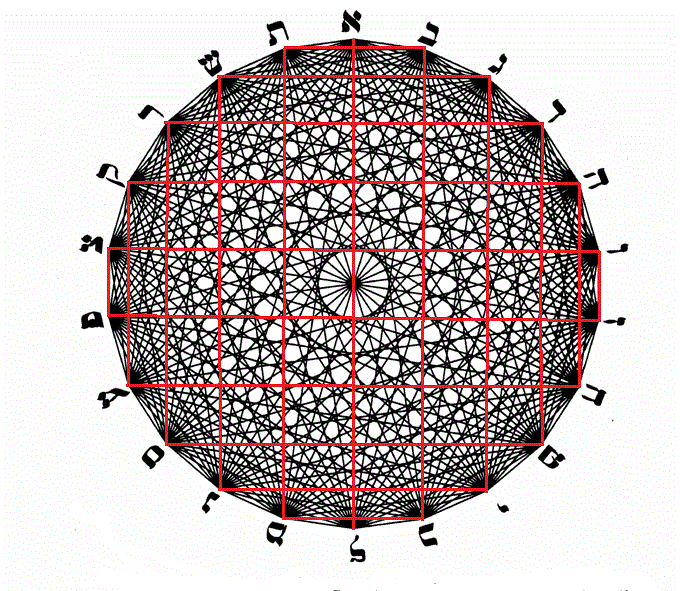 Voilà qui devrait plaire à la plus exigeante des équerres !
Voilà qui devrait plaire à la plus exigeante des équerres !
Mais, bigre, comment donc relier harmonieusement entre elles toutes ces lignes ?

Mais, bigre, comment donc relier harmonieusement entre elles toutes ces lignes ?

Montaléchel- Nombre de messages : 173
Date d'inscription : 25/07/2008
 Re: Tracer le cercle avec l'équerre
Re: Tracer le cercle avec l'équerre
L'équerre, elle est normale, à angle droit et à 90°C... Et on la tient comme une équerre normale, non comme un compas.

(Je fais durer le suspense)
(Je fais durer le suspense)

VillaChicoubis- Nombre de messages : 83
Date d'inscription : 21/02/2012
 Re: Tracer le cercle avec l'équerre
Re: Tracer le cercle avec l'équerre
90°Celsius ? 
Ainsi, on a enfin mesuré la température d'ébullition de l'angle droit !
Ainsi, on a enfin mesuré la température d'ébullition de l'angle droit !


Laposse- Nombre de messages : 242
Age : 55
Date d'inscription : 05/04/2008
 Re: Tracer le cercle avec l'équerre
Re: Tracer le cercle avec l'équerre
J'ai dit : j'ai abandonné les maths à l'équation avec 01 inconnue.
La preuve c'est que je fais pas la différence entre 90 degrés et 90°C.
Au moins je suis authentique
La preuve c'est que je fais pas la différence entre 90 degrés et 90°C.
Au moins je suis authentique

VillaChicoubis- Nombre de messages : 83
Date d'inscription : 21/02/2012
 Re: Tracer le cercle avec l'équerre
Re: Tracer le cercle avec l'équerre
Avant que les angles à 90 degrés deviennent des angles à 90°C, peut-être qu'on pourrait commencer comme cela...
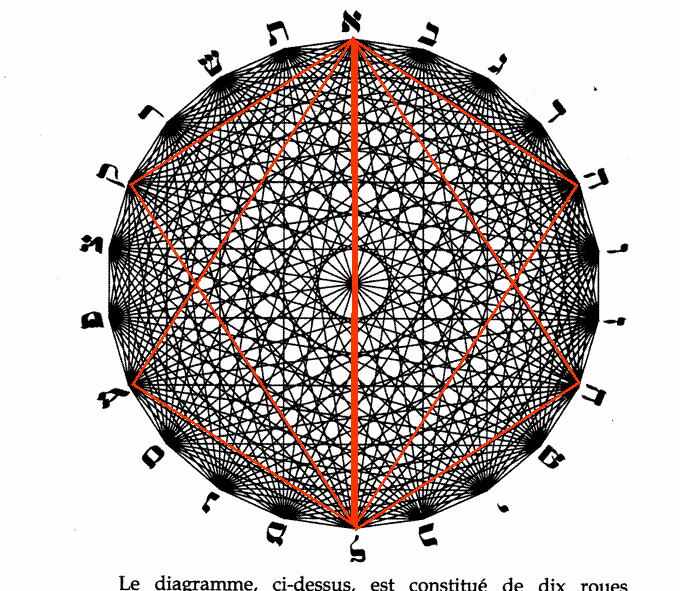


VillaChicoubis- Nombre de messages : 83
Date d'inscription : 21/02/2012
 Re: Tracer le cercle avec l'équerre
Re: Tracer le cercle avec l'équerre
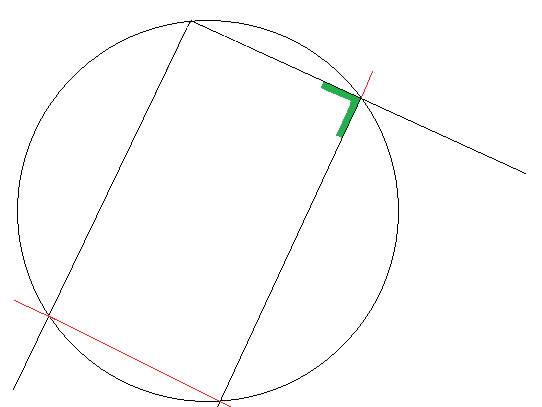
Mais alors... Montaléchel est donc sur la bonne piste, puisque ces deux rectangles traversés par un diamètre se retrouvent parmi les rectangles qu'il a mis en évidence (moyennant une petite rotation, ce qui est logique avec un cercle) :


Henri Schersch- Nombre de messages : 330
Age : 54
Date d'inscription : 21/07/2008
 Re: Tracer le cercle avec l'équerre
Re: Tracer le cercle avec l'équerre
Bonjour à tous.
Je ne suis pas vraiment sur la bonne piste, contrairement à ce que laisse entendre Henri. Je vous explique pourquoi.
Partons de rien d'autre qu'une page blanche.
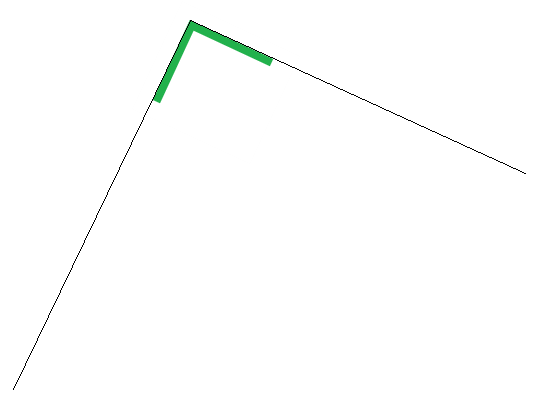
Construisons d'abord une équerre quelconque. Je la choisis verte.
 Avec cette équerre, je trace deux traits, dans l'idée de construire un premier rectangle :
Avec cette équerre, je trace deux traits, dans l'idée de construire un premier rectangle :
 Et puis…
Et puis…
Et puis... quoi ?
Ces droites ne peuvent ainsi courir jusqu'à l'infini. Il faut bien les interrompre quelque part, afin de fermer le rectangle !
Ah ! Si seulement nous disposions déjà du cercle, nous pourrions définir des intersections, et donc achever notre premier rectangle :
 Seulement voilà : la règle du jeu veut qu'on obtienne le cercle en fin de partie, et non au début. Pas de compas, qu'on a dit.
Seulement voilà : la règle du jeu veut qu'on obtienne le cercle en fin de partie, et non au début. Pas de compas, qu'on a dit.
Et puis, plus loin, comment choisir l'angle de décalage d'un deuxième rectangle par rapport au premier ? Je suis très perplexe…

Je ne suis pas vraiment sur la bonne piste, contrairement à ce que laisse entendre Henri. Je vous explique pourquoi.
Partons de rien d'autre qu'une page blanche.
Construisons d'abord une équerre quelconque. Je la choisis verte.


Et puis... quoi ?
Ces droites ne peuvent ainsi courir jusqu'à l'infini. Il faut bien les interrompre quelque part, afin de fermer le rectangle !
Ah ! Si seulement nous disposions déjà du cercle, nous pourrions définir des intersections, et donc achever notre premier rectangle :

Et puis, plus loin, comment choisir l'angle de décalage d'un deuxième rectangle par rapport au premier ? Je suis très perplexe…

Montaléchel- Nombre de messages : 173
Date d'inscription : 25/07/2008
 Re: Tracer le cercle avec l'équerre
Re: Tracer le cercle avec l'équerre
Fabrique-toi une équerre de 11 unités X 07 unités
Entre les 02 cela fera 13 unités
11 - 07 - 13
Ce n'est pas le résultat du tiercé... C'est la dimension de l'équerre que j'utilise 04 fois en la tournant et retournant.... Autour d'un axe de 13 unités.
Si je parle d'unités et non de cm, mètres, km etc...
c'est que du temps de nos anciens ils mesuraient en pouces coudées pieds etc... Or votre pouce ne mesure pas la même longueur que le mien... Donc ce qui comptait pour eux c'était avant tout l'unité... Qu'importe sa longueur exacte...
Bien à vous
Entre les 02 cela fera 13 unités
11 - 07 - 13
Ce n'est pas le résultat du tiercé... C'est la dimension de l'équerre que j'utilise 04 fois en la tournant et retournant.... Autour d'un axe de 13 unités.
Si je parle d'unités et non de cm, mètres, km etc...
c'est que du temps de nos anciens ils mesuraient en pouces coudées pieds etc... Or votre pouce ne mesure pas la même longueur que le mien... Donc ce qui comptait pour eux c'était avant tout l'unité... Qu'importe sa longueur exacte...
Bien à vous

VillaChicoubis- Nombre de messages : 83
Date d'inscription : 21/02/2012

VillaChicoubis- Nombre de messages : 83
Date d'inscription : 21/02/2012
 Re: Tracer le cercle avec l'équerre
Re: Tracer le cercle avec l'équerre
Ah Aaaah ! Voici un indice qui suggère que l'équerre à utiliser n'est pas aussi quelconque qu'on pouvait le croire !
D'abord, pour bien nous faire comprendre par nos lecteurs qui seraient fâchés avec les maths, allons nous faire voir chez les grecs. Un peu par sympathie, eu égard au problème d'endettement chronique qui les frappe, mais surtout pour nous souvenir d'un de leurs savants antiques : Pythagore. L'homme dont le théorème est utile pour fabriquer une équerre… bleue :
théorème est utile pour fabriquer une équerre… bleue :
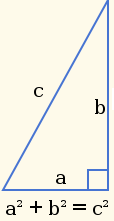 Sur les conseils de VillaChicoubis, disons donc que a vaut 7 et que b vaut 11. Il est alors facile de calculer c :
Sur les conseils de VillaChicoubis, disons donc que a vaut 7 et que b vaut 11. Il est alors facile de calculer c :
c = racine carrée de 7² + 11²
c = racine carrée de 49 + 121
c = racine carrée de 170
c = 13,03480481
Pas tout à fait 13, donc, mais allez ! Soyons bon prince, et disons que ça fait 13.
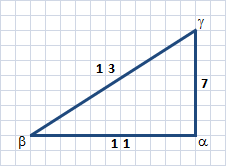
Et qu'en est-il de la valeur des angles de cette équerre bleue ?
L'angle droit vaut 90° et, puisque la somme des trois angles d'un triangle plan vaut toujours 180°, les deux autres angles restants se partagent nécessairement les autres 90°.
Pour les plus intéressés par les calculs, rappelons que la valeur d'un angle d'un triangle rectangle plan s'obtient grâce aux formules :
formules :
sin(β) = 7 / 13
sin(γ) =11 / 13
Ce qui nous donne : β = 32,5° et γ = 57,5° (à peu près, puisque la valeur 13, arrondie ci-dessus, génère un décalage).
Or, l'angle d'à peu près 32,5° est intéressant car un cercle compte 360°, et 360°/32,5° = 11. Et on voit alors la relation qui s'établit entre ce nombre 11 et la division par 22 que nous recherchons.
Les puristes lèveront les bras au ciel, à cause des "à peu près", parce que les approximations multipliées par d'autres approximations, ça finit par générer des différences franchement importantes ! De fait, l'angle de 32,5° mesure en réalité 32,4813°, et 360°/32,4813° donne 11,0833 plutôt que 11. Le double vaut donc 22,1666 et non 22,0000, mais nous avions dit que nous serions bon prince et n'allions pas chipoter pour quelques décimales, par égards pour nos ancêtres de l'antiquité, qui devaient probablement se débrouiller avec des instruments moins précis que leurs prédécesseurs bâtisseurs des pyramides de Ghizeh.
Grâce à cette équerre bleue avec des côtés valant 7,11, et 13, nous disposons maintenant d'un outil potentiellement capable de diviser le cercle en "à peu près" 22 parts égales.
Bien. Bonne idée. Attaquons-nous donc au problème par ce moyen.Fabrique-toi une équerre de 11 unités X 07 unités.
D'abord, pour bien nous faire comprendre par nos lecteurs qui seraient fâchés avec les maths, allons nous faire voir chez les grecs. Un peu par sympathie, eu égard au problème d'endettement chronique qui les frappe, mais surtout pour nous souvenir d'un de leurs savants antiques : Pythagore. L'homme dont le
 théorème est utile pour fabriquer une équerre… bleue :
théorème est utile pour fabriquer une équerre… bleue :
c = racine carrée de 7² + 11²
c = racine carrée de 49 + 121
c = racine carrée de 170
c = 13,03480481
Pas tout à fait 13, donc, mais allez ! Soyons bon prince, et disons que ça fait 13.

Et qu'en est-il de la valeur des angles de cette équerre bleue ?
L'angle droit vaut 90° et, puisque la somme des trois angles d'un triangle plan vaut toujours 180°, les deux autres angles restants se partagent nécessairement les autres 90°.
Pour les plus intéressés par les calculs, rappelons que la valeur d'un angle d'un triangle rectangle plan s'obtient grâce aux
 formules :
formules :sin(β) = 7 / 13
sin(γ) =11 / 13
Ce qui nous donne : β = 32,5° et γ = 57,5° (à peu près, puisque la valeur 13, arrondie ci-dessus, génère un décalage).
Or, l'angle d'à peu près 32,5° est intéressant car un cercle compte 360°, et 360°/32,5° = 11. Et on voit alors la relation qui s'établit entre ce nombre 11 et la division par 22 que nous recherchons.
Les puristes lèveront les bras au ciel, à cause des "à peu près", parce que les approximations multipliées par d'autres approximations, ça finit par générer des différences franchement importantes ! De fait, l'angle de 32,5° mesure en réalité 32,4813°, et 360°/32,4813° donne 11,0833 plutôt que 11. Le double vaut donc 22,1666 et non 22,0000, mais nous avions dit que nous serions bon prince et n'allions pas chipoter pour quelques décimales, par égards pour nos ancêtres de l'antiquité, qui devaient probablement se débrouiller avec des instruments moins précis que leurs prédécesseurs bâtisseurs des pyramides de Ghizeh.
Grâce à cette équerre bleue avec des côtés valant 7,11, et 13, nous disposons maintenant d'un outil potentiellement capable de diviser le cercle en "à peu près" 22 parts égales.

Montaléchel- Nombre de messages : 173
Date d'inscription : 25/07/2008
 Re: Tracer le cercle avec l'équerre
Re: Tracer le cercle avec l'équerre
Hum hum...
Vous me voyez dubitatif, mon cher Montaléchel...
Vos imprécisions ne me paraissent pas dignes de vous, ni de la tradition des tracés géométriques qui relève d'une science exacte, et non de "l'à peu près". Je connais une grande puissance nord américaine où on exécute des condamnés jugés "à peu près" coupables.
Dans ces imprécisions, je ne reconnais pas la signature de la tradition.
De même en va-t-il avec le dessin de "talisman" proposé par VillaChicoubis. Les deux triangles entrecroisés sont bien inscrits dans le cercle divisés en 22 parts, mais ils ne forment pas le traditionnel Seau de Salomon. Pour faire ressortir l'évidence, il suffit d'extraire la figure du dessin, de la jaunir un petit peu et de la faire pivoter : il devient rapidement clair que les "pointes" de l'étoile à 6 branches ne sont pas identiques, il y a des grosses et des maigres.

Trop d'imprécisions pour que cette piste soit la bonne, mon cher Montaléchel.
Vous me voyez dubitatif, mon cher Montaléchel...
Vos imprécisions ne me paraissent pas dignes de vous, ni de la tradition des tracés géométriques qui relève d'une science exacte, et non de "l'à peu près". Je connais une grande puissance nord américaine où on exécute des condamnés jugés "à peu près" coupables.
Dans ces imprécisions, je ne reconnais pas la signature de la tradition.
De même en va-t-il avec le dessin de "talisman" proposé par VillaChicoubis. Les deux triangles entrecroisés sont bien inscrits dans le cercle divisés en 22 parts, mais ils ne forment pas le traditionnel Seau de Salomon. Pour faire ressortir l'évidence, il suffit d'extraire la figure du dessin, de la jaunir un petit peu et de la faire pivoter : il devient rapidement clair que les "pointes" de l'étoile à 6 branches ne sont pas identiques, il y a des grosses et des maigres.

Trop d'imprécisions pour que cette piste soit la bonne, mon cher Montaléchel.

Sherlock- Nombre de messages : 78
Date d'inscription : 09/04/2008
 Re: Tracer le cercle avec l'équerre
Re: Tracer le cercle avec l'équerre
Je serai nettement moins sévère que Sherlock …
Même si l'échelle de celui qui monte semble tordue... Elle ne l'est pas...
Posez vous la question : Je suis une pioche en math et suis incapable de comprendre aucune des formules de Montaléchelle et pas même une équation avec 1 inconnue.
Pourtant j’arrive à résoudre une équation qui implique 22 inconnues en cercle dans le néant.
Comment je peux opérer intellectuellement si ce n’est par un changement de dialectique ?
La dialectique, c’est la pierre philosophale pour ceux qui veulent convertir leur plomb en or et souvent c'est ce qui pose le plus de problèmes au cours de cette expérience. Il faudra un jour faire comprendre aux adeptes que ce n'est pas le symbole en lui-même qui compte, mais sa dialectique....
C'est dur de reconditionner l'humain, de l'empêcher de penser cartésien, rationnel, démontrable par A + B, pour à la place penser tout simplement logique, un peu comme un animal.... Celà implique en lui une régression contre-productive au progrès selon son entendement moderne... Or, si on regarde de près la dialectique d’un lemniscate, ou d’un 08, on se rend compte que la boucle doit toujours s'achever à son point d'origine, pour reformer une nouvelle boucle... Comme si le mouvement perpétuel s'inscrivait dans un aller-retour qui tourne toujours en rond....
Si je vous parle de la dialectique et de retour aux dialectiques primitives, c'est pour attirer votre attention sur votre art de raisonner car ce n'est pas avec une dialectique moderne au carré, qu'on trace un cercle de 22 points dans lequel l’étoile à 06 branches est inévitablement déformée, (ou peut-être qu’elle retourne à son origine ?... Car je soupçonne l'imperfection de l'oeil de l'homme de l'avoir dénaturée avec le temps, cette fameuse étoile à 06 branches. Y’a de quoi faire tousser les puristes à dire cela, je sais bien, mais en kabbale juive, c’est pas des cercles de 08, 16 ou 32 points qu’on trace, mais de 22 ).
Donc ce n'est pas avec une dialectique cartésienne, mais avec une dialectique logique et pragmatique comme celle de la kabbale que non seulement on apprend à tracer ce cercle, mais également à en comprendre toute la portée qui, conformément à l’image rendue, est multidimensionnelle...
Et quand on veut envoyer son esprit à travers le multidimensionnel, cet exercice de traçage de cercle via 22 points pour faire apparaître en tout 10 cercles est tout simplement "formateur".
Nous sommes donc en présence d’un exercice de dialectique, c’est un pur retour à la synthèse kabbaliste, car tout simplement ce dessin n'est rien d'autre que "l'image" de ce que le sepher yetsirah exprime en mots....
"Par trente deux sentiers merveilleux de la sagesse s'établit la Sagesse de Yah Yhwh Dieu d'Israel (...) Son univers fut créé par trois mesures : Le nombre, l'écrit et le commentaire"
Nous apprenons donc que le Big Boss, le Grand Architecte, bref le Créateur, serait susceptible de raisonner non pas en nombres... mais en mesure de nombres !
Mesurer les nombres, voilà une indication intéressante pour notre dialectique.... Et si on se replace dans le contexte d'une époque où le mètre laser n'existait pas, on peut se demander : concrétement, comment ils faisaient pour mesurer surtout avec des pieds, des pouces et des coudées différentes d'un être humain à l'autre ? Et bien ils utilisaient ce qu'ils avaient : des lianes, des brins tressés d'herbes ou de laines. Ils mesuraient la longueur : celà donnait 11 pouces, 07 pieds ou 13 coudées selon le besoin ou le repère.
Et quand on voulait juste la demi-longueur, on repliait en deux le brin ou la tige de repère ; pour le tiers, on repliait en trois etc.... Et ainsi on avait des mesures précises basées sur des nombres mathématiques... sans se soucier des unités... Puisque juste la mesure et le nombre comptent....
Dix séphiroth dans le néant qui correspondent à 10 choses infinies sans limite… Et pour cause…. C’est le créateur qui est à l’œuvre, d’où que non seulement cet objet rond à 22 points reliès offre toutes les perspectives possibles, mais qu’il est aussi la synthèse de toutes les formes. (« Avec elles, il a représenté tout ce qui a été formé et tout ce qui sera formé », d’où que dans le fatras l’étoile à 06 branches égalitaires existe mais se fait confondre par celles aux branches non égalitaires… En cherchant bien vous trouverez aussi plusieurs formes d’étoiles à 05, 04, 03 branches et en bref toutes les formes… )
Là où cela devient intéressant c’est au 2.4 du sepher yetsirah (ce qui fait 06 justement en gématrie) quand on nous précise qu’avec ces 22 lettres, le créateur fait un cercle tel un mur ayant 231 portes (ce dessin comporte 231 traits au total) et que ce cercle oscille de l’avant vers l’arrière…
Les virgules poussières découvertes par Montaléchelle ne pourraient-elles pas trouver explication dans cette oscillation d’avant-arrière ? Autrement dit : la marge de la vibration.
Ce qui rendrait alors le calcul de Montaléchelle démentiellement précis.
D’autant que le sepher se conclut sur une chose qui devrait interpeller les alchimistes modernes, puisqu’au final, les 22 lettres, le créateur les plonge dans l’eau, les brûle au feu, les agite avec le souffle, il les enflamme de 07 planètes, et dirige avec elle les 12 constellations…
N’avez-vous jamais pensé que le pierre philosophale, après avoir été transformée en or, pouvait revenir à la pierre sous forme de diamant, qui en plus de l’éclat comme l’or, a la couleur de la lumière, est « invincible » car incassable et vibre comme le cristal ?…
Ne pensez-vous pas qu’en traçant tous ces repères, on ressemble à des joailliers en train de concevoir la taille d’un diamant ?….
Conclusion : il n’y a qu’en maniant une équerre de 7 x 11 devant une feuille blanche avec le sepher en renfort, voire un bout de ficelle en plus, qu’on comprend toute la dimension de ce dessin…
Donc j'invite Montaléchelle à continuer de monter, comme cela ; en échange moi j'apprends les maths...
Bien à vous tous
Même si l'échelle de celui qui monte semble tordue... Elle ne l'est pas...
Posez vous la question : Je suis une pioche en math et suis incapable de comprendre aucune des formules de Montaléchelle et pas même une équation avec 1 inconnue.
Pourtant j’arrive à résoudre une équation qui implique 22 inconnues en cercle dans le néant.
Comment je peux opérer intellectuellement si ce n’est par un changement de dialectique ?
La dialectique, c’est la pierre philosophale pour ceux qui veulent convertir leur plomb en or et souvent c'est ce qui pose le plus de problèmes au cours de cette expérience. Il faudra un jour faire comprendre aux adeptes que ce n'est pas le symbole en lui-même qui compte, mais sa dialectique....
C'est dur de reconditionner l'humain, de l'empêcher de penser cartésien, rationnel, démontrable par A + B, pour à la place penser tout simplement logique, un peu comme un animal.... Celà implique en lui une régression contre-productive au progrès selon son entendement moderne... Or, si on regarde de près la dialectique d’un lemniscate, ou d’un 08, on se rend compte que la boucle doit toujours s'achever à son point d'origine, pour reformer une nouvelle boucle... Comme si le mouvement perpétuel s'inscrivait dans un aller-retour qui tourne toujours en rond....
Si je vous parle de la dialectique et de retour aux dialectiques primitives, c'est pour attirer votre attention sur votre art de raisonner car ce n'est pas avec une dialectique moderne au carré, qu'on trace un cercle de 22 points dans lequel l’étoile à 06 branches est inévitablement déformée, (ou peut-être qu’elle retourne à son origine ?... Car je soupçonne l'imperfection de l'oeil de l'homme de l'avoir dénaturée avec le temps, cette fameuse étoile à 06 branches. Y’a de quoi faire tousser les puristes à dire cela, je sais bien, mais en kabbale juive, c’est pas des cercles de 08, 16 ou 32 points qu’on trace, mais de 22 ).
Donc ce n'est pas avec une dialectique cartésienne, mais avec une dialectique logique et pragmatique comme celle de la kabbale que non seulement on apprend à tracer ce cercle, mais également à en comprendre toute la portée qui, conformément à l’image rendue, est multidimensionnelle...
Et quand on veut envoyer son esprit à travers le multidimensionnel, cet exercice de traçage de cercle via 22 points pour faire apparaître en tout 10 cercles est tout simplement "formateur".
Nous sommes donc en présence d’un exercice de dialectique, c’est un pur retour à la synthèse kabbaliste, car tout simplement ce dessin n'est rien d'autre que "l'image" de ce que le sepher yetsirah exprime en mots....
"Par trente deux sentiers merveilleux de la sagesse s'établit la Sagesse de Yah Yhwh Dieu d'Israel (...) Son univers fut créé par trois mesures : Le nombre, l'écrit et le commentaire"
Nous apprenons donc que le Big Boss, le Grand Architecte, bref le Créateur, serait susceptible de raisonner non pas en nombres... mais en mesure de nombres !
Mesurer les nombres, voilà une indication intéressante pour notre dialectique.... Et si on se replace dans le contexte d'une époque où le mètre laser n'existait pas, on peut se demander : concrétement, comment ils faisaient pour mesurer surtout avec des pieds, des pouces et des coudées différentes d'un être humain à l'autre ? Et bien ils utilisaient ce qu'ils avaient : des lianes, des brins tressés d'herbes ou de laines. Ils mesuraient la longueur : celà donnait 11 pouces, 07 pieds ou 13 coudées selon le besoin ou le repère.
Et quand on voulait juste la demi-longueur, on repliait en deux le brin ou la tige de repère ; pour le tiers, on repliait en trois etc.... Et ainsi on avait des mesures précises basées sur des nombres mathématiques... sans se soucier des unités... Puisque juste la mesure et le nombre comptent....
Dix séphiroth dans le néant qui correspondent à 10 choses infinies sans limite… Et pour cause…. C’est le créateur qui est à l’œuvre, d’où que non seulement cet objet rond à 22 points reliès offre toutes les perspectives possibles, mais qu’il est aussi la synthèse de toutes les formes. (« Avec elles, il a représenté tout ce qui a été formé et tout ce qui sera formé », d’où que dans le fatras l’étoile à 06 branches égalitaires existe mais se fait confondre par celles aux branches non égalitaires… En cherchant bien vous trouverez aussi plusieurs formes d’étoiles à 05, 04, 03 branches et en bref toutes les formes… )
Là où cela devient intéressant c’est au 2.4 du sepher yetsirah (ce qui fait 06 justement en gématrie) quand on nous précise qu’avec ces 22 lettres, le créateur fait un cercle tel un mur ayant 231 portes (ce dessin comporte 231 traits au total) et que ce cercle oscille de l’avant vers l’arrière…
Les virgules poussières découvertes par Montaléchelle ne pourraient-elles pas trouver explication dans cette oscillation d’avant-arrière ? Autrement dit : la marge de la vibration.
Ce qui rendrait alors le calcul de Montaléchelle démentiellement précis.
D’autant que le sepher se conclut sur une chose qui devrait interpeller les alchimistes modernes, puisqu’au final, les 22 lettres, le créateur les plonge dans l’eau, les brûle au feu, les agite avec le souffle, il les enflamme de 07 planètes, et dirige avec elle les 12 constellations…
N’avez-vous jamais pensé que le pierre philosophale, après avoir été transformée en or, pouvait revenir à la pierre sous forme de diamant, qui en plus de l’éclat comme l’or, a la couleur de la lumière, est « invincible » car incassable et vibre comme le cristal ?…
Ne pensez-vous pas qu’en traçant tous ces repères, on ressemble à des joailliers en train de concevoir la taille d’un diamant ?….
Conclusion : il n’y a qu’en maniant une équerre de 7 x 11 devant une feuille blanche avec le sepher en renfort, voire un bout de ficelle en plus, qu’on comprend toute la dimension de ce dessin…
Donc j'invite Montaléchelle à continuer de monter, comme cela ; en échange moi j'apprends les maths...
Bien à vous tous

VillaChicoubis- Nombre de messages : 83
Date d'inscription : 21/02/2012
 sur le bon chemin?
sur le bon chemin?
C'est fascinant! 
Merci VillaChicoubis


Et tout d'abord, désolé pour mon orthographe et ma grammaire, ma dialectique et mes maths; "cancre du fond de classe" : aurait été plus juste comme nom d'utilisateur.
J'ai dessiné deux cercles de même rayon reliés par leurs centres réspectifs.
Est-ce un bon début ?
Merci VillaChicoubis
Et tout d'abord, désolé pour mon orthographe et ma grammaire, ma dialectique et mes maths; "cancre du fond de classe" : aurait été plus juste comme nom d'utilisateur.
J'ai dessiné deux cercles de même rayon reliés par leurs centres réspectifs.
Est-ce un bon début ?
lainsofor- Nombre de messages : 4
Date d'inscription : 14/03/2012
 Re: Tracer le cercle avec l'équerre
Re: Tracer le cercle avec l'équerre
Bonjour lainsofor.
Bienvenue ici.
J'ignore si tu es dans le bon avec tes deux cercles, parce que VillaChicoubis a fixé comme préalable qu'il ne fallait pas utiliser de compas ! Même un "compas" primitif constitué d'une ficelle (liane, fil de lin) pivotant autour d'un bâton fiché dans le sol ne peut pas être autorisé dans notre cas, semble-t-il.
Pourtant, il a d'abord fallu un compas (ou équivalent rustique) pour fabriquer l'angle droit de l'équerre, comme je l'expliquais dans ce premier post de Tracer le cercle avec l'équerre. Mais une fois l'équerre obtenue, ici, nous devons partir de l'idée que, par malchance, nous avons entretemps perdu le compas.
Tracer le cercle avec l'équerre. Mais une fois l'équerre obtenue, ici, nous devons partir de l'idée que, par malchance, nous avons entretemps perdu le compas.
Peut-être pourrais-tu ajouter un dessin pour mieux exposer ton idée ?
Bienvenue ici.
J'ignore si tu es dans le bon avec tes deux cercles, parce que VillaChicoubis a fixé comme préalable qu'il ne fallait pas utiliser de compas ! Même un "compas" primitif constitué d'une ficelle (liane, fil de lin) pivotant autour d'un bâton fiché dans le sol ne peut pas être autorisé dans notre cas, semble-t-il.
Pourtant, il a d'abord fallu un compas (ou équivalent rustique) pour fabriquer l'angle droit de l'équerre, comme je l'expliquais dans ce premier post de
 Tracer le cercle avec l'équerre. Mais une fois l'équerre obtenue, ici, nous devons partir de l'idée que, par malchance, nous avons entretemps perdu le compas.
Tracer le cercle avec l'équerre. Mais une fois l'équerre obtenue, ici, nous devons partir de l'idée que, par malchance, nous avons entretemps perdu le compas.Peut-être pourrais-tu ajouter un dessin pour mieux exposer ton idée ?

Calcédoine- Admin
- Nombre de messages : 325
Date d'inscription : 02/04/2008
Page 1 sur 2 • 1, 2 
A la croisée des chemins :: Les sujets du blogforum :: Sujets connexes :: Géométrie et mathématique sacrées
Page 1 sur 2
Permission de ce forum:
Vous ne pouvez pas répondre aux sujets dans ce forum

